کارشناسی ارشد

 دوره كارشناسي ارشد رشته رياضيات با دو گرايش محض و كاربردي جهت تربيت متخصصاني است كه بتوانند برمباني علوم رياضي و فنون مدون در اين رشته احاطه يافته، با كسب مهارتهاي علمي و عملي لازم به تعليم دراين رشته بپردازند. حداكثر طول مجاز تحصيلات اين دوره 2 سال است كه اين مدت شامل وقت لازم جهت اتمام پايان‌نامه نيز مي‌باشد. تعداد كل واحدهاي تخصصي جهت فراغت از تحصيل 32 واحد درسي است كه در هر يك از دو گرايش محض و كاربردي ارائه مي‌شود.
تعداد واحدهاي الزامي 12 واحد، تعداد واحدهاي اختياري 12 واحد، گذراندن 2 واحد سمينار و گذراندن 6 واحد پايان‌نامه الزامي است.

 

دروس الزامي كارشناسي ارشد رياضي محض

 

---

نام درس	تعداد واحد
آناليز حقيقي	4
جبر پيشرفته 3	4
هندسه منيفلد 1	4

 

 

دروس اختياري تخصصي كارشناسي ارشد رياضي محض

 

---

نام درس	تعداد واحد
جبر جابجايي	4
جبر و گروه لي 1	4
نظريه نمايش گروه‌ها	4
آناليز تابعي	4
توپولوژي ديفرانسيل 1	4
هندسه منيفلد 2	4
گروههاي متناهي	4
نظريه كاتگوري	4
توپولوژي ديفرانسيل	4
نظريه جبري اعداد	4
گروههاي جايگشتي	4
نظريه تحليلي اعداد	4

 

نتایج مسابقات ریاضی

با عرض سلام خدمت دوستان

با کمال تاسف باید عرض کنم که با تمام امیدی که امسال به دانشگاهمون  داشتیم تیم دانشگاه ملایر با ۵ پله سقوط نسبت به سال گذشته در رتبه ۳۱ مسابقات دانشجویی ریاضی کشور قرار گرفت.
از نکات جالب تیم دانشگاه ما این بود که وقتی یکی از دانشجوا به یکی از سوالات درست جواب داده بود و به تیم داوری اعتراض داشت هر چه قدر اون جواب رو برای سرپرست تیم توضیح می داد متوجه نمیشد.(سرپرست تیم جناب آقای دکتر!! مهری بود).
البته پایین تر از تیم ما هم دانشگاه های مطرحی قرار داشتن.از جمله دانشگاه بین المللی قزوین دانشگاه زنجان دانشگاه مازندران و ...
دانشگاه اول مثل همیشه دانشگاه صنعتی شریف بود که با تیم دوم(دانشگاه تهران)اختلاف امتیاز خیلی زیادی داشت.تیم آخر(یعنی تیم
 ۴۱ام) هم تیم دانشگاه آزاد واحد قایم شهر بود.
برای مشاهده کامل  نتایج میتونید به لینکهای زیر مراجعه کنید:

نتایج تیمی مسابقات

نتایج انفرادی مسابقات

نحس بودن عدد 13

اگر از كوچه پس كوچه‌های قديمی شهرآنجايی كه هنوز رگه‌هايی از خانه‌های قديمی كاهگلی يافت می‌شود گذر كنيم هنوز هم پلاكهای خانه‌هايی را می توان ديد كه روی آن 1+12 به جای سيزده نوشته شده است، علت آن را در اعتقادات مردم می توان يافت تحت اين عنوان:
نحس بودن 13 !
آنچه در ادامه خواهيد خواند جادوی 13 است كه به نظر جالب می رسد !!!
● 13 عدد اول است.
● 1-13^2 عدد اول مرسن است. 
13جسم ارشميدسی موجود است. (اجسام ارشميدسی اجسامی هستند كه وجوه آنها چند ضلعی بوده، نه لزوما از يك نوع ، و كنجهای آنها مساوی هستند.) 
عدد 13كوچكترين Emirp است. (Emirp عدد اولی است كه اگر ارقام آن را معكوس كنيم مجددا عددی اول خواهد بود مثلا اعداد 13، 17،31، 37،.....)
● 169=2^13 بامعكوس كردن ارقام آن داريم: 961="2^31 يعنی رقم های آن مجددا معكوس می شود."
●2^13، 1+!12 را عاد مي‌كند.
● 13عدد Happy است.(برای دانستن اين كه عددی Happy است، مجموع مربعات رقمهاي عدد را پيدا كرده و دوباره مجموع مربعات عدد بدست آمده را حساب می‌كنيم با ادامه اين روند اگر به عدد 1 دست پيدا كرديم آنگاه به آن عدد Happy گفته می‌شود. مثلا برای عدد سيزده 10="2^3+2^1 و 1=2^0+2^1 بنابراين13" عدد Happyاست.)
● 13نيمی از 3^3+ 3^1- است.
●شاخه زيتونی كه در پشت دلارهای آمريكا كشيده شده است 13 برگ دارد.
●2^13عدد !(1 -13)+ 1را عاد می‌كند بنابراين يك عدد اول ويلسون(Wilson Prime) است. ( هر عدد اول p كه،p و p^2، مقدار p-1)!+1 ) را عاد كنند، عدد اول ويلسون ناميده می‌شود. مثلا عدد 5 عدد ويلسون است. تنها اعداد شناخته شده 5 و 13و 563 است .)
●چرتكه چينی دارای سيزده ستون مهره‌ برای محاسبات است.
● 13بزرگترين عدد اولی است كه می تواند به دو عدد متوالی به صورت n^2+3 افراز می شود.(آيا می توانيد اثبات کنيد؟)
● 1+13- 13^13 عدد اول است.
برای خواندن بقیه خصوصیات عدد ۱۳ بر روی ادامه مطلب کلیک کنید:

ادامه نوشته

رمز نگاري

سلام
امروز می خوام مقداری در مورد کاربرد ریاضیات در رمزنگاری مطلب بنویسم.یکی از معروفترین روش های رمز نگاری روش RSA ست.ميدونيد RSA به چه معنيه؟...
حروف RSA ابتدای نام سه پدید آورنده آن است:

 Ronald Rivest, Adi Shamir ,Leonard Adleman.

 

از چپ به راست Leonard Adleman، Ronald Rivest، Adi Shamir کار های اولیه بر روی RSA به زمان دانشجوی آنها در MIT بر میگردد.

این روش بر پایه ایده ای به ظاهر ساده ولی زیرکانه است که در زیر مطرح می شود:

ضرب اعداد خیلی ساده است بویژه با استفاده از رایانه ،  ولی تجزیه اعداد بسیار مشکل است. مثلا اگر بخواهیم بدانیم که حاصلضرب 34537 در 99991 چقدر می شود براحتی با وارد کردن این اعداد در ماشین حساب به عدد 3453389167 میرسیم اما عکس این عمل بسیار سخت تر است.

اگر  عدد 14459160519 را به شما داده باشند و گفته باشند که این عدد با ضرب دو عدد صحیح به دست آمده است.آیا می توانید این دو عدد را تعیین کنید.این سوال نسبتا سخت است انصافاٌ رایانه این عدد را به سرعت تجزیه میکند (البته در این کار از لم های خاصی استفاده می شود ) ، اساسا این کار با امتحان کردن تعداد زیادی ترکیب احتمالی صورت می گیرد.رایانه برای اینکه هر عدد ، با هر اندازه ای ، را تجزیه کند مجبور است تقریبا در حدود «ریشه دوم آن عدد» ترکیب احتمالی را امتحان کند.مثلا در این مورد خاص تقریبا 38000 مورد بررسی می شود.

البته بررسی 38000 احتمال برای رایانه زیاد وقت گیر نیست ولی ، اگر عدد داده شده 10 رقمی نباشد و مثلا 400 رقمی باشد چه اتفاقی می افتد؟! ریشه دوم عددی  400 رقمی تقریبا 200 رقم دارد . عمر جهان تقریبا 10¹⁸ ثانیه است یعنی یک عدد 18 رقمی . حالا فرض کنید یک رایانه بتواند هر یک میلیون ترکیب احتمالی را در یک ثانیه چک کند ، در طول عمر جهان این رایانه قادر به چک کردن 10²⁴ مورد است اما برای عدد 400 رقمی 10²⁰0 احتمال وجود دارد . به این معنی رایانه برای تجزیه این عدد 10¹⁷⁸ برابر عمر جهان مشغول به محاسبه خواهد بود.
اما چک کردن اینکه یک عدد اول است یا نه به این اندازه دشوار نیست – به عبارت دیگر امتحان کنیم که ، آیا یک عدد می تواند قابل تجزیه شدن نباشد!

RSA هم به همین ترتیب عمل می کند . ابتدا دو عدد اول بسیار بزرگ ، p و q،پیدا می کنیم بطوری که هر کدام 100 یا 200 رقم داشته باشد. این اعداد محرمانه هستند ( در واقع همان کلید خصوصی ما هستند ) ، سپس این اعداد را در هم ضرب می کنیم تا عدد N=p.q ساخته شود .اساسا عدد N ی که به این ترتیب ساخته می شود کلید عمومی ما تلقی می شود. رسیدن به عدد N نسبتا کار ساده ای برای ما خواهد بود ، اما اگر شخصی بخواهد عدد N را تجزیه کند کار بسیار مشکل و تقریبا غیر ممکنی برایش خواهد بود.

فرمول اعداد اول

فرمول اعداد اول
این فرمول توسط یک استاد ریاضی ایرانی (آقای سید محمد رضا هاشمی موسوی) پیشنهاد شده است.

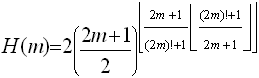
برای اطلاعات بیشتر به لینک زیر مراجعه کنید:

h t t p : / / w w w . p r i m e n u m b e r s f o r m u l a . c o m

هشتمین مسابقه دانشجویی آمار کشور

هشتمین مسابقه‌ي دانشجويي آمار كشور توسط گروه آمار دانشگاه مازندران با همكاري انجمن آمار ايران و پژوهشكده‌ي آمار در سیزدهم شهريورماه 1386 برگزار مي‌شود.
شرايط شركت در مسابقه، نحوه‌‌‌ي ثبت‌نام و هزينه‌ي آن
1- زمان برگزاري مسابقه روزسیزدهم شهريور ماه 1386 صبح و عصراست.
2- هزينه‌ي ثبت‌نام براي هر تيم و سرپرست آن ( جمعاً 4 نفر ) مبلغ 3000000 ريال است، كه بايد به حساب شماره‌ي 952948172 نزد بانك تجارت (شعبه باجه دانشگاه مازندران) به نام سمیناراحتمال و فرآیندهای تصادفی بابت شركت در ششمین سمینار احتمال و فرآیندهای تصادفی و هشتمين مسابقه‌ي دانشجويي آمار كشور واريز گردد و اصل فيش به همراه اسامي تيم شركت‌كننده، سرپرست آنها و فرم‌هاي ثبت‌نام تكميل شده حداكثر تا تاريخ 30/3/86 به آدرس مسابقه ارسال گردد.
3- اعضاي تيم مسابقه و سرپرست محترم در ششمین سمینار احتمال و فرآیندهای تصادفی نيز ثبت‌نام شده و مي‌توانند شركت نمايند.

بازی آشوب

مثلث سیرپینسکی

 

 

احتمالا شما هم چیزهایی درباره‌ی سیستم‌های آشوب‌ناک (Chaotic) شنیده‌اید.

 

 در این پست می‌خوام یک بازی ریاضی آشوب‌ناک و جالب را به شما معرفی کنم. با این بازی به‌سادگی

 

 می‌تونید با یک برنامه‌ی کامپیوتری مثلث سیرپینسکی را بکشید. خب اول بگم بازی چه جوریه . یک

 

کاغذ سفید بردارید و یک مثلث بزرگ روی آن بکشید. سه گوشه‌ی مثلث را با اعداد ۱ تا ۳ شماره‌گذاری

 

کنید. حالا نقطه‌ی دل‌خواه P را روی صفحه‌ی کاغذ بکشید. بعد یک گوشه‌ی تصادفی از مثلث را انتخاب

 

کنید، مثلا. نقطه‌ای که دقیقن وسط نقطه‌ی P و گوشه‌ی ۳ مثلث باشد را پیدا کنید و اسم‌اش را Q

 

بگذارید. دوباره یک گوشه‌ی تصادفی ازمثلث را انتخاب کنید و نقطه‌ی وسط این گوشه و Q را پیدا کنید و

 

اسم‌اش را R بگذارید. اگر همین کار را هزاران بار تکرار کنید، شکلی شبیه شکل زیر به دست می‌آید.

 

 خیلی جالب هست، نه؟ 

 

 اسم این شکل مثلث سیرپینسکی (Sierpinski) هست. نکته‌ی جالب‌تر اینه که

 

 مهم نیست نقطه‌ی P که اول انتخاب کرده بودید، کجای صفحه باشه. این روند همیشه منجر به تولید

 

مثلث سیرپینسکی می‌شه. نکته‌ی جالب دیگه این هست که ترتیب انتخاب گوشه‌های مثلث اصلی هم

 

 اهمیتی نداره. 

با تشکر از دوست خوبمون نویسنده وبلاگ هنر هشتم ریاضیات

نهمین کنفرانس آموزش ریاضی ایران

نهمین کنفرانس آموزش ریاضی ایران از ۱۷ الی ۱۹ شهریور ماه در دانشگاه سیستان و بلو چستان برگزار می شود.برخی از اهداف و برنامه های کنفرانس به شرح ذیل می باشد:

● برنامه كنفرانس :

  سخنراني عمومي، ارائه مقالات (سخنراني، پوستر)، كارگاه، نمايشگاه و ميز گرد.

---

● موضوعات مورد بحث :

1- بهبود وضعيت آموزش رياضي و چالشهاي پيش روي

  - مباني نظري آموزش رياضي.                              

  - بررسي عوامل مؤثر در پيشرفت تحصيلي رياضي.      

  - اهداف و محتواي برنامه هاي درسي .                       

  - روشهاي ياددهي و يادگيري علوم رياضي .             

  - جايگاه آموزش رياضي در نظام آموزشي.

  - ارزشيابي پيشرفت تحصيلي و برنامه هاي درسي.

  - ديدگاهها و رويكردها به نقش ICT  در آموزش رياضي.

  - رابطه تاريخ رياضي و آموزش رياضي.

  - نقش آموزش ابتدایی در شکل گیری مفاهیم ریاضی.

2- آموزش معلمان رياضي:

  - آموزش حرفه اي قبل و ضمن خدمت معلمان رياضي.

  - آموزش تخصصي قبل و ضمن خدمت معلمان رياضي.

  - پژوهش ها و تجربه هاي تدريس معلمان در ارتباط با كلاس درس.

3- برنامه هاي جانبي:

  - برگزاري نمايشگاه ( كتاب ـ انتشارات ـ دست سازه ها).

  - كارگاه ها ( Farsi Tex  ـ حل مساله ـ مقاله نویسی - خلاقیت ).

  - معرفی فعالیتهای غیر رسمی ریاضی (وبلاگ نويسي ـ آموزش مجازی ـ  ...  ).

برای اطلاعات بیشتر در مورد کنفرانس می توانید به لینک زیر مراجعه کنید:

نهمین کنفرانس آموزش ریاضی ایران

مسابقات دانشجویی

سلام خدمت همه دوستان
همونطور که اطلاع دارید مسابقات دانشجویی سی یکمین دوره اون از ۲۰تا ۲۳ اردیبهشت ماه در دانشگاه فردوسی مشهد در حال برگزاری است.
آزمون در دو نوبت و در روزهای بیستم و بیست ویکم برگزار شده و مسابقات مراحل پایانشو داره پشت سر می ذاره.
البته امسال امیدواری ها به دانشگاهه ما خیلی زیاده(با حضور آقای آذرمهر و آقای فصیحی) و انتظار میره که دانشگاهه ما در بین ۱۰ دانشگاه برتر قرار بگیره.
علاقه مندانی که دوست دارن سوالات رو ببین(یا حل کنن!)میتونن به لینک های
زیر مراجه کنن....

سوالات نوبت اول

 سوالات نوبت دوم

سال اویلر

 

هیچ میدونستین سال ۲۰۰۷ سال اویلره؟

انجمن ریاضی امریکا به مناسبت  300امین سالگرد تولد اویلر، ریاضیدان بزرگ

 سوئیسی، سال 2007 را سال اویلر نامگذاری نموده است.

لئونارد اویلر، که یکی از بزرگترین ریاضیدانان در تمام اعصار به شمار می­رود،

 15آوریل 1707 در باسل سوئیس متولد شد. او در تاریخ بلند ریاضیات چهره­ای

 بسیار برجسته است. پس از پایان تحصیلات در زادگاه، او به سنت­پترزبورگ

 روسیه و پس از آن به آکادمی برلین نقل مکان کرد.

به دلیل مشارکت در تمامی شاخه­های ریاضیات، بیش از 25000 مقاله از او به­جا مانده است. رکوردی که به نظر غیرقابل دستیابی می­نماید.